题目描述

在一个 $n×m$ 的棋盘上有一颗黑色棋子和一颗白色棋子。你有无限次机会，每次将其中的一颗棋子向上、下、左、右任意一个方向移动任意格，但在移动时，另一颗棋子也会向相同的方向移动相同的距离。

在整个过程中，若某次移动会导致黑棋或白棋超出棋盘范围，则此次移动是不合法的。

容易发现：在每次移动都合法的前提下，棋盘上总会有一些“无法抵达的格子”，即：不管黑棋还是白棋，无论如何都不可能移动到这些格子上。

给出棋盘大小以及黑白棋子的初始坐标$(x_1,y_1),(x_2,y_2)$。请你计算有多少个无法抵达的格子。

输入格式：

$6$ 个整数 $n,m,x_1,y_1,x_2,y_2$，含义与题目中相同。

输出格式

一个整数，表示无法抵达的格子的数量。

样例

4 4 1 1 3 3

8

4 3 1 1 2 2

2

2 2 1 2 2 1

2

样例 $1$ 解释

棋盘的大小为 $4×4$，黑色棋子所在的位置是 $(1,1)$，白色棋子所在的位置是 $(3,3)$。在合法移动的前提下，它们可以在下图蓝色区域内自由移动：

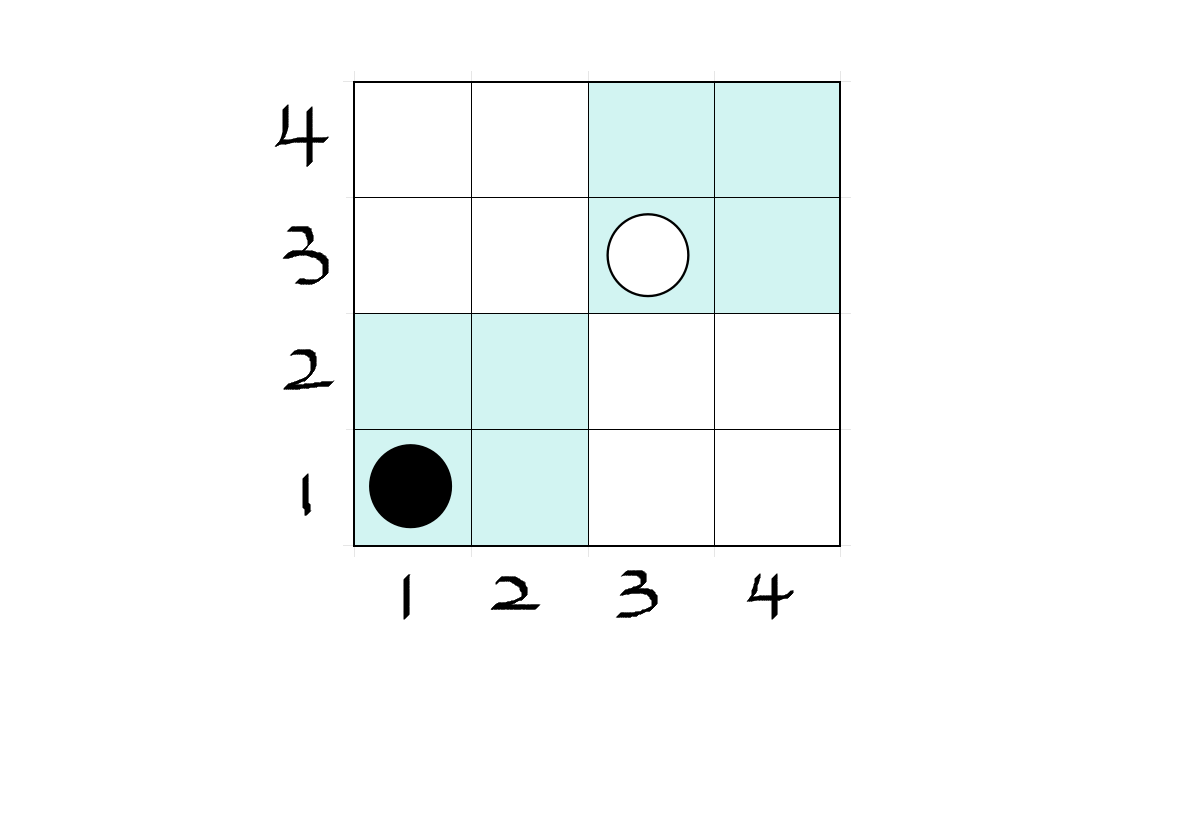
因此无法抵达的格子有 $8$ 个，即所有白色格子。

数据规模与约定

对于 $60\%$ 的数据，$1≤x_i,y_i≤n,m≤100$；

对于另外 $20\%$ 的数据，保证两颗棋子初始时处在同一行或同一列；

对于 $100\%$ 的数据，$1≤x_i,y_i≤n,m≤10^9$，且保证两颗棋子的初始位置不重叠。