该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

题目描述

本题的目标是求一个点数无穷的无向图的桥。

这个无向图具有如下性质：

1. 这个图是一个连通图。

2. 这个图的所有节点分为若干层，分别是第$1$层、第$2$层、第$3$层$\cdots$共有无穷层，每层共有$n$个节点。为了描述方便，以下用$(i, x)$表示第$i$层的$x$号节点。

3. 同一层内的节点可以相互连边，相邻两层的节点之间可以相互连边，除此之外，其他节点之间不能相互连边。

4. 如果$(i, x)$与$(i, y)$之间有一条权值为$d$的边，那么$(j, x)$与$(j, y)$之间也有一条边，它的权值为$0.9^{j-i}d$，其中j为任意正整数。

5. 如果$(i, x)$与$(i + 1, y)$之间有一条权值为$d$的边，那么$(j, x)$与$(j+1, y)$之间也有一条边，它的权值为$0.9^{j-i}d$，其中$j$为任意正整数。如下所示的无向图就符合上面的所有性质。

一个点数无穷的无向图是连通的，当且仅当对于图中的任意两个节点都存在一条路径将它们连接起来。而一条边是桥，当且仅当这条边被删去后整个图不连通。

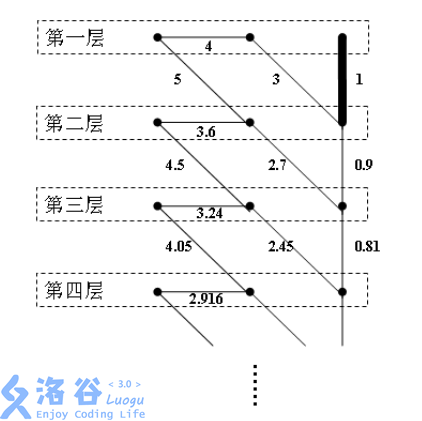
请你编写程序读入这个点数无穷的连通图，求出其中所有桥的权值之和。例如，在上图中，粗线所示的边就是该图唯一的桥，因此上图中桥的权值之和为$1$。

输入格式

输入文件infinite.in第一行包括三个由空格隔开的非负数$n$、$m_1$、$m_2$。从第$2$行到第$m_1+ 1$行，每行有三个正整数$x$、$y$、$d$，表示$(1, x)$与$(1, y)$之间有一条权值为d的边。

从第$m_1+ 2$行到第$m_1+ m_2+ 1$行，每行有三个正整数$x$、$y$、$d$，表示$(1, x)$与$(2, y)$之间有一条权值为$d$的边。每行的三个整数之间都用一个空格隔开。

图中两个点$x$和$y$之间可能有多于$1$条边连接，一条边连接的两个节点可能相同。

输出格式

输出文件infinite.out只有一行，包含一个实数，即所有桥的权值之和，四舍五入保留两位小数。

3 1 3
1 2 4
1 2 5
2 3 3
3 3 1

1.00

1 1 1
1 1 100
1 1 1

10.00

提示

【样例说明1】

这就是问题描述中所举的例子。

【数据规模】 ||||| | :----------- | :----------- | :----------- | :----------- | | 数据编号 | $n$ | $m_1$ | $m_2$ | | 1 | $\leq10$ | $\leq50$ | $\leq50$ | | 2 | $\leq10000$ | $\leq40000$ | $\leq40000$ | | 3 | $\leq300000$ | $\leq500000$ | $=1$ | | 4~7 | $\leq300000$ | $\leq500000$ | $\leq500$ | | 8~10 | $\leq300000$ | $\leq500000$ | $\leq500000$ |

100%的数据中，$d\leq 100$。